语文
I.考试性质
普通高等学校招生全国统一考试是由合格的高中毕业生参加的选拔性考试。高等学校根据考生的成绩。按已确定的招生计划,德、智、体全面衡量,择优录取。因此,高考应有较高的信度、效度,必要的区分度和适当的难度。
II.考试能力要求
高考语文要求测试识记、理解、分析综合、表达应用和鉴赏评价五种能力。这五种能力表现为五个层级。
A.识记指识别和记忆,是语文能力最基本的层级。
B.理解指领会并能作简单的解释,是在识记基础上高一级的能力层级。
C.分析综合指分解剖析和归纳整理,是在识记和理解的基础上进一步提高了的能力层级。
D.表达应用指对语文知识和能力的运用,是识记、理解和分析综合为基础,在表达方面发展了的能力层级。
E.鉴赏评价指对阅读材料的鉴别、赏析和评说,是以识记、理解和分析综合为基础,在阅读方面发展了的能力层级。
对A、B、C、 D、E五个能力层级均可有难易不同的考查。
Ⅲ.考试内容
考试内容及相应的能力层级如下:
一、语言知识和语言表达
能识记基本的语言知识,掌握常见的语言表达技能。
1.识记A
①识记现代汉语普通话的字音
②识记现代汉字的字形
2.表达应用D
①正确使用标点符号
②正确使用词语(包括熟语)
③辨析并修改病句
病句类型:语序不当、搭配不当、成分残缺或赘余、结构混乱;表意不明、不合逻辑
④扩展语句,压缩语段。
⑤选用、仿用、变换句式
⑥语言表达简明、连贯、得体
⑦正确运用常见的修辞方法
常见修辞方法:比喻、比拟、借代、夸张、对偶、排比、设问、反问。
二、文掌常识和名句名篇
能识记文学常识,默写常见的名句名篇.
识记A
①识记中国重要作家及其时代和代表作
②识记外国重要作家及其时代和代表作
③识记文学体裁常识
④默写常见的名句名篇
三、古代诗文阅读
能阅读浅易的古代诗文.
1.理解B
①理解常见文言实词在文中的含义
②理解常见文言虚词在文中的用法
常见文言虚词:而、何、乎、乃、其、且、若、所、为、焉、也、以、因、于、与、则、者、之。
③理解与现代汉语不同的句式和用法
不同的句式和用法:判断句、被动句、宾语前置、成分省略和词类活用。
④理解并翻译文中的句子
2.分析综合C
①筛选文中的信息
②归纳内容要点,概括中心意思
③分析慨括作者在文中的观点态度
3.鉴赏评价E
①鉴赏文学作品的形象、语言和表达技巧
②评价文章的思想内容和作者的观点态度
四、现代文阅读
能阅读一般社会科学类、自然科学类文章和文学作品。
1.理解B
①理解文中重要词语的含义
②理解文中重要句子的含意
2.分析综合C
①筛选并整合文中的信息
②分析文章结构,把握文章思路
③归纳内容要点,概括中心意思
④分析概括作者在文中的观点态度
⑤根据文章内容进行推断和想像
3.鉴赏评价E
①鉴赏文学作品的形象、语言和表达技巧
②评价文章的思想内容和作者的观点态度
五、写作
能写记叙文、议论文、说明文及其他常见体裁的文章。
作文考试的要求分为基础和发展两个等级。
1.基础等级D
①符合题意
②符合文体要求
③感情真挚,思想健康
④内容充实,中心明确
⑤语言通顺,结构完整
⑥书写规范,标点正确:
2.发展等级D
①深刻
透过现象深入本质,揭示问题产生的因果关系.
②丰富
材料丰富,形象丰满,意境深远.
③有文采
词语生动,句式灵活,善于运用修辞手法,文句有意蕴.
④有创新
见解新颖,材料新鲜,构思新巧,推理想像有独到之处,有个性色彩.
Ⅳ考试形式
答卷方式:闭卷,笔试。试卷满分为15O分.考试限定用时为150分钟。
考试题型:单项选择题、多项选择题、古文翻译题、埴空题、简答题、写作题。
数学(文科)
Ⅰ.考试性质
普通高等学校招生全国统一考试是由合格的高中毕业生和具有同等学力的考生参加的选拔性考试,高等学校根据考生的成绩,按已确定的招生计划,德、智、体、全面衡量,择优录取,因此,高等应有较高的信度、效度、必要的区分度和适当的难度.
Ⅱ.考试能力要求
1.平面向量
考试内容:
向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离.平移.
考试要求:
(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念.
(2)掌握向量的加法和减法.
(3)掌握实数与向量的积,理解两个向量共线的充要条件.
(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.
(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.
(6)掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式.
2.集合、简易逻辑
考试内容:
集合.子集.补集.交集.并集.
逻辑联结词.四种命题.充分条件和必要条件.
考试要求:
(1)理解集合、子集、补集、交集、并集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.掌握有关的术语和符号,并会用它们正确表示一些简单的集合.
(2)理解逻辑联结词“或”、“且”、“非”的含义.理解四种命题及其相互关系.掌握充分条件、必要条件及充要条件的意义.
3.函数
考试内容:
映射.函数.函数的单调性.奇偶性.
反函数.互为反函数的函数图像间的关系.
指数概念的扩充.有理指数幂的运算性质.指数函数.
对数.对数的运算性质.对数函数.
函数的应用.
考试要求:
(1)了解映射的概念,理解函数的概念.
(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法.
(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数.
(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质.
(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.
(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.
4.不等式
不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式.
考试要求:
(1)理解不等式的性质及其证明.
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单的不等式.
(4)掌握简单不等式的解法.
(5)理解不等式│a│-│b│≤│a+b│≤│a│+│b│.
5.三角函数
考试内容:
角的概念的推广.弧度制.
任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.
两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.
正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx+)的图像.正切函数的图像和性质.已知三角函数值求角.
正弦定理.余弦定理.斜三角形解法.
考试要求:
(1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.
(2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.
(3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.
(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+)的简图,理解A,ω,的物理意义.
(6)会由已知三角函数值求角,并会用符号arcsin x、arccos x、arctanx表示.
(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.
6.数列
考试内容:
数列.
等差数列及其通项公式.等差数列前n项和公式.
等比数列及其通项公式.等比数列前n项和公式.
考试要求:
(1)理解数列的概念,了解数列通项公式的意义.了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.
(2)理解等差数列的概念,掌握等差数列的通项公式与前n项和公式,并能解决简单的实际问题.
(3)理解等比数列的概念,掌握等比数列的通项公式与前n项和公式,并能解决简单的实际问题.
7.直线和圆的方程
考试内容:
直线的倾斜角和斜率.直线方程的点斜式和两点式.直线方程的一般式.
两条直线平行与垂直的条件.两条直线的交角.点到直线的距离.
用二元一次不等式表示平面区域.简单的线性规划问题.
曲线与方程的概念.由已知条件列出曲线方程.
圆的标准方程和一般方程.圆的参数方程.
考试要求:
(1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程.
(2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系.
(3)了解二元一次不等式表示平面区域.
(4)了解线性规划的意义,并会简单的应用.
(5)了解解析几何的基本思想,了解坐标法.
(6)掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程.
8.圆锥曲线方程
考试内容:
椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程.
双曲线及其标准方程.双曲线的简单几何性质.
抛物线及其标准方程.抛物线的简单几何性质.
考试要求:
(1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,了解椭圆的参数方程.
(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质.
(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质.
(4)了解圆锥曲线的初步应用.
9(A).①直线、平面、简单几何体
考试内容:
平面及其基本性质.平面图形直观图的画法.
平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.
平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求:
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.
(2)掌握两条直线平行与垂直的判定定理和性质定理.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.
(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直的判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.
(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角的平面角、两个平行平面间的距离的概念.掌握两个平面垂直的判定定理和性质定理.
(5)会用反证法证明简单的问题.
(6)了解多面体、凸多面体的概念,了解正多面体的概念.
(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.
(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
9(B).直线、平面、简单几何体
考试内容:
平面及其基本性质.平面图形直观图的画法.
平行直线.
直线和平面平行的判定与性质.直线和平面垂直的判定.三垂线定理及其逆定理.
两个平面的位置关系.
空间向量及其加法、减法与数乘.空间向量的坐标表示.空间向量的数量积.
直线的方向向量.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面垂直的性质.平面的法向量.点到平面的距离.直线和平面所成的角.向量在平面内的射影.
平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定和性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求:
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系.
(2)掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念,掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理.
(3)理解空间向量的概念,掌握空间向量的加法、减法和数乘.
(4)了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算.
(5)掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式.
(6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.
(7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念.对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离.掌握直线和平面垂直的性质定理.掌握两个平面平行、垂直的判定定理和性质定理.
(8)了解多面体、凸多面体的概念,了解正多面体的概念.
(9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(10)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.
(11)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
(考生可在9(A)和9(B)中任选其一)
10.排列、组合、二项式定理
考试内容:
分类计数原理与分步计数原理.
排列.排列数公式.
组合.组合数公式.组合数的两个性质.
二项式定理.二项展开式的性质.
考试要求:
(1)掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题.
(2)理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.
(3)理解组合的意义,掌握组合数计算公式和组合数的性质,并能用它们解决一些简单的应用问题.
(4)掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题.
11.概率
考试内容:
随机事件的概率.等可能性事件的概率.互斥事件有一个发生的概率.相互独立事件同时发生的概率.独立重复试验.
考试要求:
(1)了解随机事件的发生存在着规律性和随机事件概率的意义.
(2)了解等可能性事件的概率的意义,会用排列组合的基本公式计算一些等可能性事件的概率.
(3)了解互斥事件、相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率.
(4)会计算事件在n次独立重复试验中恰好发生k次的概率.
12.统计
考试内容:
抽样方法.总体分布的估计.
总体期望值和方差的估计.
考试要求:
(1)了解随机抽样了解分层抽样的意义,会用它们对简单实际问题进行抽样.
(2)会用样本频率分布估计总体分布.
(3)会用样本估计总体期望值和方差.
13.导数
考试内容:
导数的背景.
导数的概念.
多项式函数的导数.
利用导数研究函数的单调性和极值.函数的最大值和最小值.
考试要求:
(1)了解导数概念的某些实际背景.
(2)理解导数的几何意义.
(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.
(5)会利用导数求某些简单实际问题的最大值和最小值.
Ⅲ.考试形式与试卷结构
考试采用闭卷、笔试形式.全卷满分为150分,考试时间为120分钟.
全试卷包括Ⅰ卷和Ⅱ卷.Ⅰ卷为选择题;Ⅱ卷为非选择题.
试卷一般包括选择题、填空题和解答题等题型.选择题是四选一型的单项选择题;填空题只要求直接填写结果,不必写出计算过程或推证过程;解答题包括计算题、证明题和应用题等,解答应写出文字说明、演算步骤或推证过程.
试卷应由容易题、中等题和难题组成,总体难度要适当,并以中等题为主。
数学(理科)
Ⅰ.考试性质
普通高等学校招生全国统一考试是由合格的高中毕业生和具有同等学力的考生参加的选拔性考试,高等学校根据考生的成绩,按已确定的招生计划,德、智、体、全面衡量,择优录取,因此,高等应有较高的信度、效度、必要的区分度和适当的难度.
Ⅱ.考试能力要求
1.平面向量
考试内容:
向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离.平移.
考试要求:
(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念.
(2)掌握向量的加法和减法.
(3)掌握实数与向量的积,理解两个向量共线的充要条件.
(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.
(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.
(6)掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式.
2.集合、简易逻辑
考试内容:
集合.子集.补集.交集.并集.
逻辑联结词.四种命题.充分条件和必要条件.
考试要求:
(1)理解集合、子集、补集、交集、并集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.掌握有关的术语和符号,并会用它们正确表示一些简单的集合.
(2)理解逻辑联结词“或”、“且”、“非”的含义.理解四种命题及其相互关系.掌握充分条件、必要条件及充要条件的意义.
3.函数
考试内容:
映射.函数.函数的单调性.奇偶性.
反函数.互为反函数的函数图像间的关系.
指数概念的扩充.有理指数幂的运算性质.指数函数.
对数.对数的运算性质.对数函数.
函数的应用.
考试要求:
(1)了解映射的概念,理解函数的概念.
(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法.
(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数.
(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质.
(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.
(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.
4.不等式
不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式.
考试要求:
(1)理解不等式的性质及其证明.
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单的不等式.
(4)掌握简单不等式的解法.
(5)理解不等式│a│-│b│≤│a+b│≤│a│+│b│.
5.三角函数
考试内容:
角的概念的推广.弧度制.
任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.
两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.
正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx+)的图像.正切函数的图像和性质.已知三角函数值求角.
正弦定理.余弦定理.斜三角形解法.
考试要求:
(1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.
(2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.
(3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.
(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+)的简图,理解A,ω,的物理意义.
(6)会由已知三角函数值求角,并会用符号arcsin x、arccos x、arctanx表示.
(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.
6.数列
考试内容:
数列.
等差数列及其通项公式.等差数列前n项和公式.
等比数列及其通项公式.等比数列前n项和公式.
考试要求:
(1)理解数列的概念,了解数列通项公式的意义.了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.
(2)理解等差数列的概念,掌握等差数列的通项公式与前n项和公式,并能解决简单的实际问题.
(3)理解等比数列的概念,掌握等比数列的通项公式与前n项和公式,并能解决简单的实际问题.
7.直线和圆的方程
考试内容:
直线的倾斜角和斜率.直线方程的点斜式和两点式.直线方程的一般式.
两条直线平行与垂直的条件.两条直线的交角.点到直线的距离.
用二元一次不等式表示平面区域.简单的线性规划问题.
曲线与方程的概念.由已知条件列出曲线方程.
圆的标准方程和一般方程.了解参数方程的概念.圆的参数方程.
考试要求:
(1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程.
(2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系.
(3)了解二元一次不等式表示平面区域.
(4)了解线性规划的意义,并会简单的应用.
(5)了解解析几何的基本思想,了解坐标法.
(6)掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程.
8.圆锥曲线方程
考试内容:
椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程.
双曲线及其标准方程.双曲线的简单几何性质.
抛物线及其标准方程.抛物线的简单几何性质.
考试要求:
(1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,了解椭圆的参数方程.
(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质.
(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质.
(4)了解圆锥曲线的初步应用.
9(A).①直线、平面、简单几何体
考试内容:
平面及其基本性质.平面图形直观图的画法.
平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.
平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求:
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.
(2)掌握两条直线平行与垂直的判定定理和性质定理.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.
(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直的判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.
(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角的平面角、两个平行平面间的距离的概念.掌握两个平面垂直的判定定理和性质定理.
(5)会用反证法证明简单的问题.
(6)了解多面体、凸多面体的概念,了解正多面体的概念.
(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.
(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
9(B).直线、平面、简单几何体
考试内容:
平面及其基本性质.平面图形直观图的画法.
平行直线.
直线和平面平行的判定与性质.直线和平面垂直的判定.三垂线定理及其逆定理.
两个平面的位置关系.
空间向量及其加法、减法与数乘.空间向量的坐标表示.空间向量的数量积.
直线的方向向量.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面垂直的性质.平面的法向量.点到平面的距离.直线和平面所成的角.向量在平面内的射影.
平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定和性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求:
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系.
(2)掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念,掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理.
(3)理解空间向量的概念,掌握空间向量的加法、减法和数乘.
(4)了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算.
(5)掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式.
(6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.
(7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念.对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离.掌握直线和平面垂直的性质定理.掌握两个平面平行、垂直的判定定理和性质定理.
(8)了解多面体、凸多面体的概念,了解正多面体的概念.
(9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(10)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.
(11)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
(考生可在9(A)和9(B)中任选其一)
10.排列、组合、二项式定理
考试内容:
分类计数原理与分步计数原理.
排列.排列数公式.
组合.组合数公式.组合数的两个性质.
二项式定理.二项展开式的性质.
考试要求:
(1)掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题.
(2)理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.
(3)理解组合的意义,掌握组合数计算公式和组合数的性质,并能用它们解决一些简单的应用问题.
(4)掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题.
11.概率
考试内容:
随机事件的概率.等可能性事件的概率.互斥事件有一个发生的概率.相互独立事件同时发生的概率.独立重复试验.
考试要求:
(1)了解随机事件的发生存在着规律性和随机事件概率的意义.
(2)了解等可能性事件的概率的意义,会用排列组合的基本公式计算一些等可能性事件的概率.
(3)了解互斥事件、相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率.
(4)会计算事件在n次独立重复试验中恰好发生k次的概率.
12.概率与统计
考试内容:
离散型随机变量的分布列. 离散型随机变量的期望值和方差.
抽样方法.总体分布的估计.正态分布.线性回归.
考试要求:
(1)了解离散型随机变量的意义,会求出某些简单的离散型随机变量的分布列.
(2)了解离散型随机变量的期望值、方差的意义,会根据离散型随机变量的分布列求出期望值、方差.
(3)会用随机抽样、系统抽样、分层抽样等常用的抽样方法从总体中抽取样本.
(4)会用样本频率分布去估计总体分布.
(5)了解正态分布的意义及主要性质.
(6)了解线性回归的方法和简单应用.
13.极限
考试内容:
教学归纳法.数学归纳法应用.
数列的极限.
函数的极限.根限的四则运算.函数的连续性.
(1)理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.
(2)了解数列极限和函数极限的概念.
(3)掌握极限的四则运算法则;会求某些数列与函数的极限.
(4)了解函数连续的意义,了解闭区间上连续函数有最大值和最小值的性质.
14.导数
考试内容:
导数的概念.导数的几何意义.几种常见函数的导数.
两个函数的和、差、积、商和导数.复习函数的导数.基本导数公式.
利用导数研究函数的单调性和极值.函数的最大值和最小值.
考试要求:
(1)了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念.
(2)熟记基本导数公式;掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数.
(3)理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值.
15.数系的扩充-复数
考试内容:
复数的概念.
复数的加法和减法.
复数的乘法和除法.
数系的扩充.
考试要求:
(1)了解复数的有关概念及复数的代数表示和几何意义.
(2)掌握复数代数形式的运算法则,能进行复数代数形式的加法、减法、乘法、除法运算.
(3)了解从自然数系到复数系的关系及扩充的基本思想.
Ⅲ.考试形式与试卷结构
考试采用闭卷、笔试形式.全卷满分为150分,考试时间为120分钟.
全试卷包括Ⅰ卷和Ⅱ卷.Ⅰ卷为选择题;Ⅱ卷为非选择题.
试卷一般包括选择题、填空题和解答题等题型.选择题是四选一型的单项选择题;填空题只要求直接填写结果,不必写出计算过程或推证过程;解答题包括计算题、证明题和应用题等,解答应写出文字说明、演算步骤或推证过程.
试卷应由容易题、中等题和难题组成,总体难度要适当,并以中等题为主.
英语
Ⅰ.考试性质
普通高等学校招生全国统一考试是由合格的高中毕业生和具有同等学力的考生参加的选拔性考试。高等学校根据考生的成绩,按已确定的招生计划,德、智、体全面衡量,择优录取。因此,高考应有较高的信度、效度、必要的区分度和适当的难度。
英语科考试是按照标准化测试要求设计的。
Ⅱ.考试内容和要求
根据普通高等学校对新生文化素质的要求,参照教育部2000年颁发的《全日制高级中学英语教学大纲(试验修订版)》,并考虑中学教学实际,制订本学科考试内容。
一、语言知识
要求考生能够适当运用基本的语法知识(见附录),掌握2000左右的词汇及相关词组(见《全日制高级中学英语教学大纲(试验修订版)》)
二、语言运用
1.听力
要求考生听懂有关日常生活中所熟悉话题的简短独白和对话。考生应能:
(1)理解主旨要义;
(2)获取事实性的具体信息;
(3)对所听内容作出简单推断;
(4)理解说话者的意图、观点或态度。
2.阅读
要求考生读懂公告、说明、广告以及书、报、杂志中关于一般性话题的简短文章。考生应能:
(1)理解主旨要义;
(2)理解文中具体信息;
(3)根据上下文推断生词的词义;
(4)作出简单判断和推理;
(5)理解文章的基本结构;
(6)理解作者的意图和态度。
3.写作
要求考生根据题示进行书面表达。考生应能:
(1)准确使用语法和词汇;
(2)使用一定的句型、词汇,清楚、连贯地表达自己的意思。
Ⅲ.考试形式与试卷结构
1.答卷方式:闭卷、笔试。
2.考试时间:120分钟。试卷满分为150分。
3.题型:试卷一般包括多项选择题、完形填空题、填空题、短文改错和书面表达等题型。
4.试题难易比例:试卷包括容易题、中等题和难题,以中等题为主。
Ⅳ.题型示例
一、多项选择题
(一)考查听力
M:Well, I wonder why the office is still not open .
W:But it's not yet eight. In fact, it's only a quarter to eight.
1.At what time does the office open ?
A.7:45. B.8:15. C.8:00.
M:It's Alice's birthday tomorrow.
W:Are you sure ? I think it should be the day after tomorrow.
M:Well, let me see. Oh, I'm sorry. You're right. It is the day after tomorrow. Shall we buy her a present?
W:Yes, of course. Shall we give her some flowers?
M:Flowers are lovely. But I think it's better to buy her a nice box of chocolates.
W:Alice doesn't like sweet things. Didn't you know that?
M:You're right. Er…I know. We can give her a record. She loves music.
W:That's a good idea. Let's go to the music shop and choose one for her.
2.When is Alice's birthday?
A.The next day. B.The day after next. C.The day they had the talk.
3.What will the man and the woman buy for Alice ?
A.A record. B.Some flowers. C.A box of chocolates.
(二)考查语法和词汇知识
1.Paul doesn't have to be made_______.He always works hard.
A.study B.to study C.studied D.studying
2.I first met Lisa three years ago when we ______ at a radio station together.
A.have worked B.had been working C.were working D.had worked
3.She thought I was talking about her daughter,_________,in fact, I was talking about my daughter.
A.whom B.where C.which D.while
4.-When shall we meet again?
-Make it ________ day you like; it's all the same to me.
A.one B.any C.another D.some
(三)考查阅读理解
We walked in so quietly that the nurse at the desk didn't even lift here eyes from the book. Mum pointed at a big chair by the door and I knew she wanted me to sit down. While I watched, mouth open in surprise, Mum took off her hat and coat and gave them to me to hold. She walked quietly to the small room by the lift and took out a wet mop(拖把). She pushed the mop past the desk and as the nurse looked up, Mum nodded and said, "Very dirty floors."
"Yes. I'm glad they've finally decided to clean them," the nurse answered. She looked at Mum strangely and said, "But aren't you working late?"
Mum just pushed harder, each swipe(拖) of the mop taking her farther and farther down the hall. I watched until she was out of sight and the nurse had turned back to writing in the big book.
After a long time Mum came back. Her eyes were shining. She quickly put the mop back and took my hand. As we turned to go out of the door, Mum nodded politely to the nurse and said, "Thank you."
Outside, Mum told me, "Dagmar is fine. No fever."
"You saw her, Mum?"
"Of course. I told her about the hospital rules, and she will not expect us until tomorrow. Dad will stop worrying as well. It's a fine hospital. But such floors! A mop is no good. You need a brush."
1.When she took a mop from the small room, what Mum really wanted to do was______.
A.to clean the floor B.to please the nurse
C.to see a patient D.to surprise the story-teller
2.When the nurse talked to Mum, she thought Mum was a_______.
A.nurse B.visitor C.patient D.cleaner
3.After reading the story what can we infer about the hospital?
A.It is a children's hospital.
B.It has strict rules about visiting hours.
C.The nurses and doctors there don't work hard.
D.A lot of patients come to this hospital every day.
4.Why did Mum go to see Dagmar in the hospital?
A.To give her some messages about Dad.
B.To make sure her room was clean.
C.To check that she was still there.
D.To find out how she was.
5.Which of the following words best describes Mum?
A.polite B.patient C.changeable D.clever
二、完形填空题
Washoe is a young chimpanzee(黑猩猩). She is no(1)chimpanzee, though. Scientists are doing research(2)her. They want to see how civilized (驯化) she can(3). Already she can do many things a human being does.
For example, she has been learning how to exchange(4)with people. The scientists are teaching her(5)language. When she wants to be picked(6), Washoe points up with one finger. She rubs her teeth with her finger(7)she wants to brush her teeth. This is done after every meal.
Washoe has also been(8)to find answers to problems. Once she was put in a(9)with food hanging from the ceiling. It was too high to(10). After she considered the(11), she got a tall box to(12). The food was still too high to be reached. Washoe found a(13)pole. Then she climbed onto the(14), grasped (抓取)the pole, and(15)down the food with the pole.
Washoe(16)like a human, too. The scientists keep her in a fully furnished house. After a hard(17)in the lab, she goes home.(18)she plays with her toys. She(19)enjoys watching television before going to bed.
Scientists hope to(20)more about people by studying our closest relative-the chimpanzee.
1.A.foolish B.simple C.special D.ordinary
2.A.for B.on C.to D.by
3.A.experience B.change C.develop D.become
4.A.actions B.views C.messages D.feelings
5.A.human B.sign C.spoken D.foreign
6.A.out B.at C.on D.up
7.A.when B.until C.since D.while
8.A.trained B.raised C.ordered D.led
9.A.hole B.zoo C.room D.museum
10.A.pull B.see C.eat D.reach
11.A.problem B.position C.food D.ceiling
12.A.stand by B.stand on C.stand up D.stand with
13.A.straight B.strong C.long D.heavy
14.A.wall B.box C.ceiling D.pole
15.A.knocked B.picked C.took D.pulled
16.A.lives B.works C.thinks D.plays
17.A.task B.lesson C.time D.day
18.A.But B.There C.So D.Besides
19.A.quite B.already C.even D.still
20.A.see B.answer C.learn D.gain
三、听力填空题
Man:…and lastly this week I have some information about a course at the Country College near Burnside, which might be of interest to someone wanting a late-season break, or to groups. They tell me they have spaces on their Country Sports courses the weekend after next. There are three courses that you might like to join: fishing, hill-walking, and rock-climbing. So, quite a lot of variety there. The fishing is open to anyone over the age of 12, and so is the hill-walking. For the rock-climbing you must be sixteen or older, for safety reasons. All these courses are really enjoyable.
BURNSIDE COUNTRY COLLEGE
Country Sports Weekends
| COURSE |
AGE |
| Fishing |
12+ |
| 1.____________ |
2.____________ |
| Rock-climbing |
16+ |
四、短文改错题
Today I visited the Smiths-my first time visit 1. _______
to a American family. They live in a small 2. _______
town. It was very kind for them to meet me 3. _______
at the railway station and drove me to their home. 4. _______
The Smiths did his best to make me feel 5. _______
at home. They offered me coffee and other 6. _______
drinks. We have a good time talking and laughing 7. _______
together. They were eager know everything about 8. _______
China and asked me lots of question. In fact, 9. _______
they are planning to visit China in next year. 10. _______
五、书面表达题
假定你是李华。你和几个朋友约定星期天在人民公园野餐。你们的英国朋友Peter 也应邀参加。请你根据下面的示意图,给他写封短信,告诉他进公园后如何找到你们。
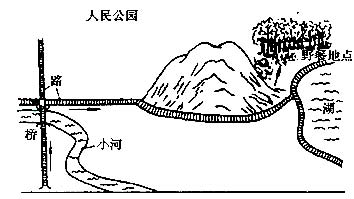
注意:
1.词数80~120;
2.开头语已为你写好。
June 1st
Dear Peter,
We're so glad you're coming to join us on Sunday. Here is how you can find us.
Li Hua
附录 语法项目表
1.词类
1)名词 2)形容词 3)副词 4)动词 5)代词 6)冠词 7)数词 8)介词 9)连词 10)感叹词
2.名词
1)可数和不可数名词 2)名词的复数形式 3)专有名词 4)所有格
3.代词
1)人称代词 2)物主代词 3)反身代词 4)指示代词 5)不定代词 6)疑问代词
4.数词
1)基数词 2)序数词
5.介词
6.连词
7.形容词
1)形容词作定语、表语和宾语补足语的用法 2)比较等级:原级、比较级、最高级
8.副词
1)时间、地点、方式、程度、疑问、连接、关系等副词的用法
2)比较等级:原级、比较级、最高级
9.冠词的一般用法
10.动词
1)动词的基本形式
(1)现在式 (2)过去式 (3)过去分词 (4)-ing形式
2)行为动词的及物性和不及物性
3)连系动词be, get, look, seem, turn, grow, become等
4)助动词be, do, have, shall, will等
5)情态动词can, may, must, ought, need, dare等
6)动词的时态
(1)一般现在时 (2)一般过去时 (3)一般将来时 (4)现在进行时 (5)过去进行时 (6)现在完成时 (7)过去完成时 (8)过去将来时
7)动词的被动语态
(1)一般现在时的被动语态 (2)一般过去时的被动语态 (3)一般将来时的被动语态 (4)现在进行时的被动语态 (5)现在完成时的被动语态 (6)带情态动词的被动语态
8)动词的不定式
(1)作主语 (2)作宾语 (3)作宾语补足语 (4)作状语 (5)作定语 (6)作表语 (7)用在how, when, where, what,which, who, whether等后面
9)动词的过去分词
(1)作定语 (2)作表语 (3)作宾语补足语 (4)作状语
10)动词的-ing形式
(1)作主语 (2)作宾语 (3)作宾语补足语 (4)作表语 (5)作定语 (6)作状语
11.句子
1)句子的种类
(1)陈述句(肯定式和否定式) (2)疑问句(一般疑问句、特殊疑问句、选择疑问句、反意疑问句) (3)祈使句 (4)感叹句
2)句子的成分
(1)主语 (2)谓语 (3)表语 (4)宾语 (5)直接宾语和间接宾语 (6)宾语补足语 (7)定语 (8)状语
3)主谓的一致关系
4)简单句的五种基本句型
5)并列句
6)复合句
(1)名词性从句 (2)状语从句 (3)定语从句
7)倒装句
8)省略句
12.构词法
1)合成法blackboard, man-made, overthrow, however, everyone
2)转换法hand(n.)-hand(v.), break(v.)-break(n.) empty(adj.)-empty(v.)
3)派生法
(1)加前缀:dis-, in-, re-, un-, non-
(2)加后缀:-able, -al, -an, -ful, -ive, -er, -ese, -st, -ment, -ness, -tion, -fy, -ian, -ing, -is(z)e, -ly, -teen, -ty, -th, -y